インタラクティブ・ブローカーズ・ホーム
手数料体系
チケットチャージ・プラットフォーム使用料無料など、低コストでご利用いただけます。
グローバルアクセス
1つの取引ツールから、世界の株式やオプション、先物およびCFDに投資して下さい。
プレミア・テクノロジー
IBKRのパワフルなテクノロジーが取引スピードと効率を最適化し、高度なポートフォリオ分析をサポートします。
財務体質および顧客資産保全
お客様の資産はすべて日々時価評価されます。IBグループの強固な財務基盤によりお客様の資産は保全されています。
IBグループ 取引ツール及びサービス受賞歴
インタラクティブ・ブローカーズ証券株式会社は、インタラクティブ・ブローカーズ・グループの子会社です。

プロフェッショナル・トレーディングの部門で第1位
インターナショナル・トレーディングの部門で第1位

アドバンス・トレーダー部門で
ベスト・オンライン・ブローカー

ベスト・オンライン・ブローカー部門において5つ星の第1位

アドバンス
トレーダー部門でベスト

ベスト・オンライン・ブローカー

プロのための価格設定をご利用ください1
- 低手数料、完全無料の取引専用ソフトウェア!
- 当社のBestXTMは、市場への影響を最小限に抑えながら、最良執行の達成と価格向上の最大化を図るようにデザインされた、パワフルで高度な取引テクノロジーです。
- 取引量・取引額に基づく段階的(Tiered)手数料体系。
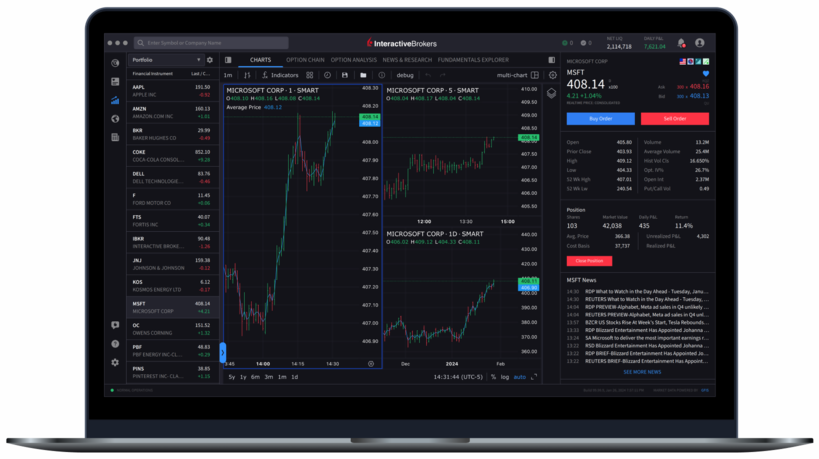
プロも驚く高機能
を備えた取引ツール
IBグループで受賞歴のある取引ツールをデスクトップ、モバイル、ウェブバージョンでご利用いただけます。
指値注文から複雑なアルゴリズム取引まで、充実した注文タイプがお客様の取引ストラテジーをサポートします。
信用できる証券会社
お客様の資金を証券会社に預け入れる際は、その会社が安全で、金融市場の好不況に左右されない耐久力をもっていることを確認する必要があります。当社は、その強固な資本基盤と財務状態、自動化されたリスク管理体制により、万一金融機関の安定性を損ないうる重大な事態が市場で起こっても、グループ全体が守られるように設計されています。
インタラクティブ・ブローカーズ証券株式会社は、インタラクティブ・ブローカーズ・グループの子会社です。
IBKR
Nasdaq上場
$161億
自己資本*
74.6%
個人所有*
$104億
自己資本余力*
312万
クライアント口座*
235万
1日の標準取引高*
IBKR保護

*インタラクティブ・ブローカーズ・グループとその関連会社。追加情報に関しましては、当社の「投資家情報」-「決算発表」をご覧ください。
ご自身にあった口座タイプをお選びください
ステップ1
口座開設のお申込み
所要時間は数分です。
ステップ 2
口座への入金
銀行口座とリンクまたは
口座移管
ステップ3
取引の開始
投資を次のレベルへ
ステップアップ
- インタラクティブ・ブローカーズ・グループおよびその前身となる関連会社の内容も含みます。詳細はこちらより、IR情報内の「Earnings Release」の項目をご確認ください。
- 「インタラクティブ・ブローカーズ・グループ」および「IBKR」は、グループ内すべての子会社を含みます。




 個人口座
個人口座 プロップ・ファーム取引口座
プロップ・ファーム取引口座 事業法人口座
事業法人口座 エンプロイー・トラック口座
エンプロイー・トラック口座 機関投資家口座
機関投資家口座